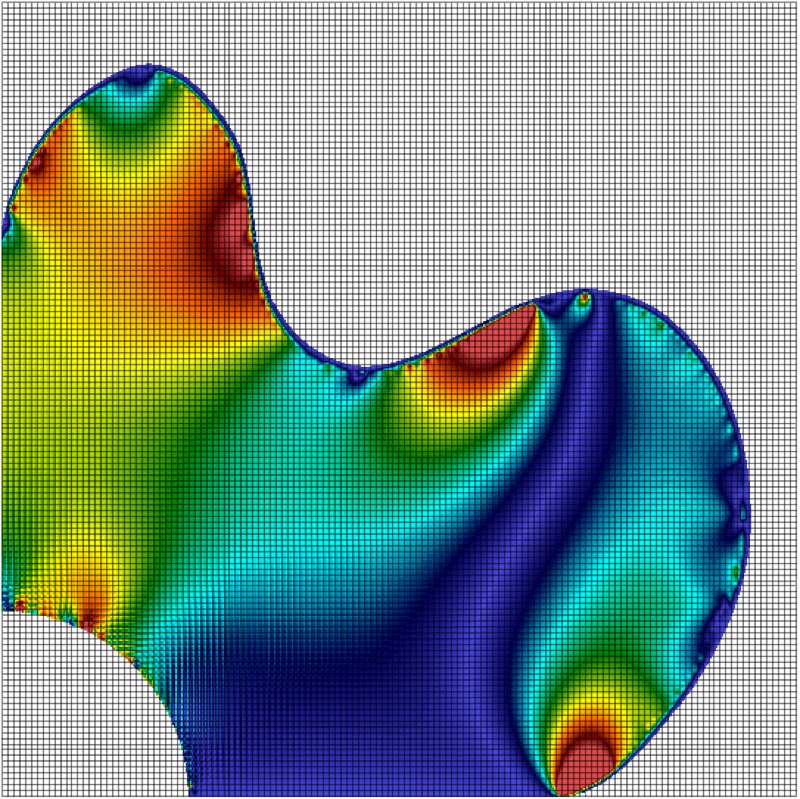
Code Structure
AMPLE’s high-level structure is below and comprises three loops:
-
a loadstep for loop that first determines the external forces at the nodes for the current step and then calculates the nodal basis functions and spatial derivatives for each material point. The code then enters a while loop to find equilibrium between the internal and external forces. Once equilibrium has been obtained the material point positions and internal variables (deformation gradient, stress, elastic logarithmic strain, domain size, etc.) are updated.
-
a Newton-Raphson while loop to solve the global equilibrium equations on the background mesh. The loop first solves the non-linear system of equations to determine the displacement and reaction force increments at the nodes before moving onto the determination of the current internal force and stiffness via a material point for loop.
-
a material point for loop that determines the internal force and stiffness contribution of each of the material points to the background mesh.

AMPLE’s main script, ample.m, is shown in its entirety below. The format of the code aligns with the algorithm shown above. Comments are shown in green and have been truncated on the right hand side for clarity of the executed code. Only two of the three loops described above can be seen in the main ample.m file: (1) a loadstep for loop spanning lines 9 through 33 and
(2) a Newton-Raphson while loop over lines 21 through 30. The material point loop is contained within the detMPs.m function on line 25.
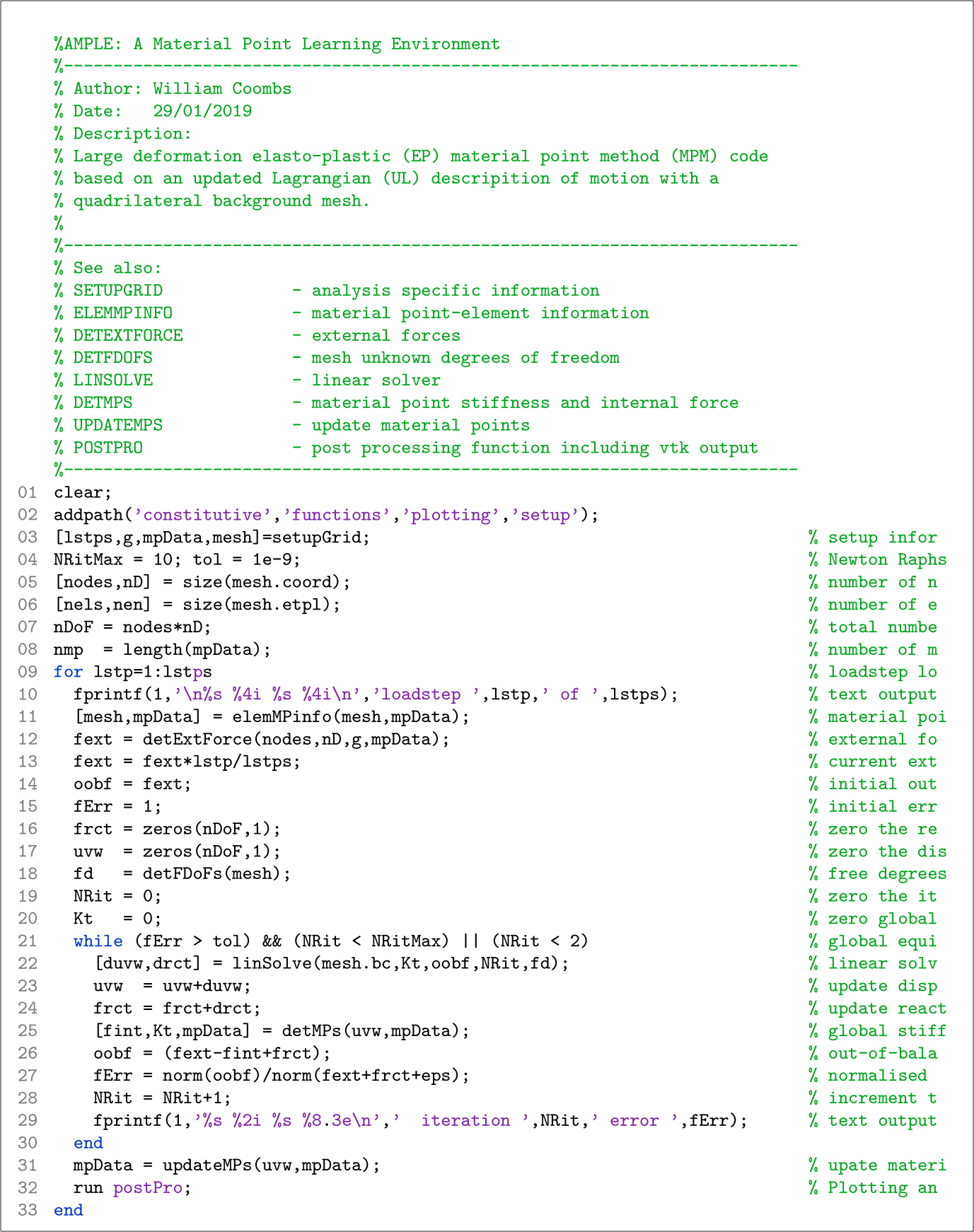
The main ample.m script calls eight functions, the purpose of each of these functions is explained below:
-
setupGrid: called on line 3 ofample.m, the function returns the analysis-specific information such as details of the background grid and any information held at material points (position, material properties, etc.). -
elemMPinfo: called on line 1 ofample.m, the function determines the parent element(s) of each material point and the nodes that the material point influences. Note that for the standard material point method each material point will only have one parent element but in the generalised interpolation material point method the domain of the point can overlap multiple elements. The function also determines the basis functions at each of the material points and their spatial gradients based on the nodal positions at the start of the load step. The function calls three other functions:elemForMPthat finds the element(s) associated with the material point,nodesForMPthat determines a unique list of nodes based on the element(s) associated with the material point andMPMbasisthat determines the basis functions for the material point. This function depends on the type of material point method and the form of the background mesh. -
detExtForce: called on line 12 ofample.m, the function determines the external force vector at the start of the load step based on the body and point forces at material points. -
detFDoFs: called on line 18 ofample.m, the function determines a list of the unknown displacement degrees of freedom of the background mesh based on the elements that contain material points and the displacement boundary conditions imposed on the mesh. -
linSolve: called on line 22 ofample.m, the function solves the linear system of equations to determine the iterative increment in the nodal displacements based on the current out-of-balance force residual. The function also determines the increment in the reaction forces due to the constrained degrees of freedom on the background mesh. -
detMPs: called on line 25 ofample.m, the function determines the stiffness and internal force contribution of each material point to the background mesh and assembles these into a global stiffness matrix and internal force vector. This function contains the updated Lagrangian formulation and the constitutive model controlling the stress-strain behaviour of each material point. The function calls three other functions:Hooke3Da linear elastic constitutive model,VMconsta linear elastic perfectly plastic von Mises constitutive model andformULstiffa function to determine the consistent spatial tangent modulus. -
updateMPs: called on line 31 ofample.m, the function updates the positions and volumes of the material points based on the incremental nodal displacements and the current value of the deformation gradient at each material point. For generalised interpolation material point methods, the function also updates the domain lengths. This function depends on the type of material point method and will require modification if a user wishes to implement other domain-based methods. -
postPro: called on line 32 ofample.m, the function produces VTK output files that can be viewed when the analysis has finished via a suitable VTK file visualised (such as VisIt or Paraview, amongst others). The function calls two functions:makeVtkandmakeVtkMPthat generate VTK files for the background mesh and the material points, respectively.
The structure of these functions is shown diagrammatically below, where the solid and dashed lines around the function boxes indicate that the function does or does not calls other functions, respectively. The black arrows indicate the function calls and the locations of the loops in the code are indicated by the grey lines. For example, Hook3d.m is called by detMPs.m; and linSolve.m and detMPs.m are called within the equilibrium, or N-R, loop.
The majority of AMPLE’s functions do not depend on: (i) the form of the background mesh, (ii) the type of material point methods adopted or (iii) the number of physical dimensions (1D, 2D plane strain or 3D). The exceptions to this are: elemMPinfo.m which depends on the background mesh type and the material point variant and updateMPs.m which depends on the material point variant as different updating procedures are required for different material point methods. Obviously setupGrid.m depends on all three of the above points as it contains the analysis-specific information that will change depending on the user’s requirements.
The functions are organised into a number of folders depending on their purpose, specifically: constitutive contains the constitutive functions, setup contains the functions that are required to provide the analysis-specific information, plotting contains the post-processing files and functions contains the remaining M files. AMPLE’s file structure also contains output and documentation that contain the generated VTK files and AMPLE’s html documentation.
Function format
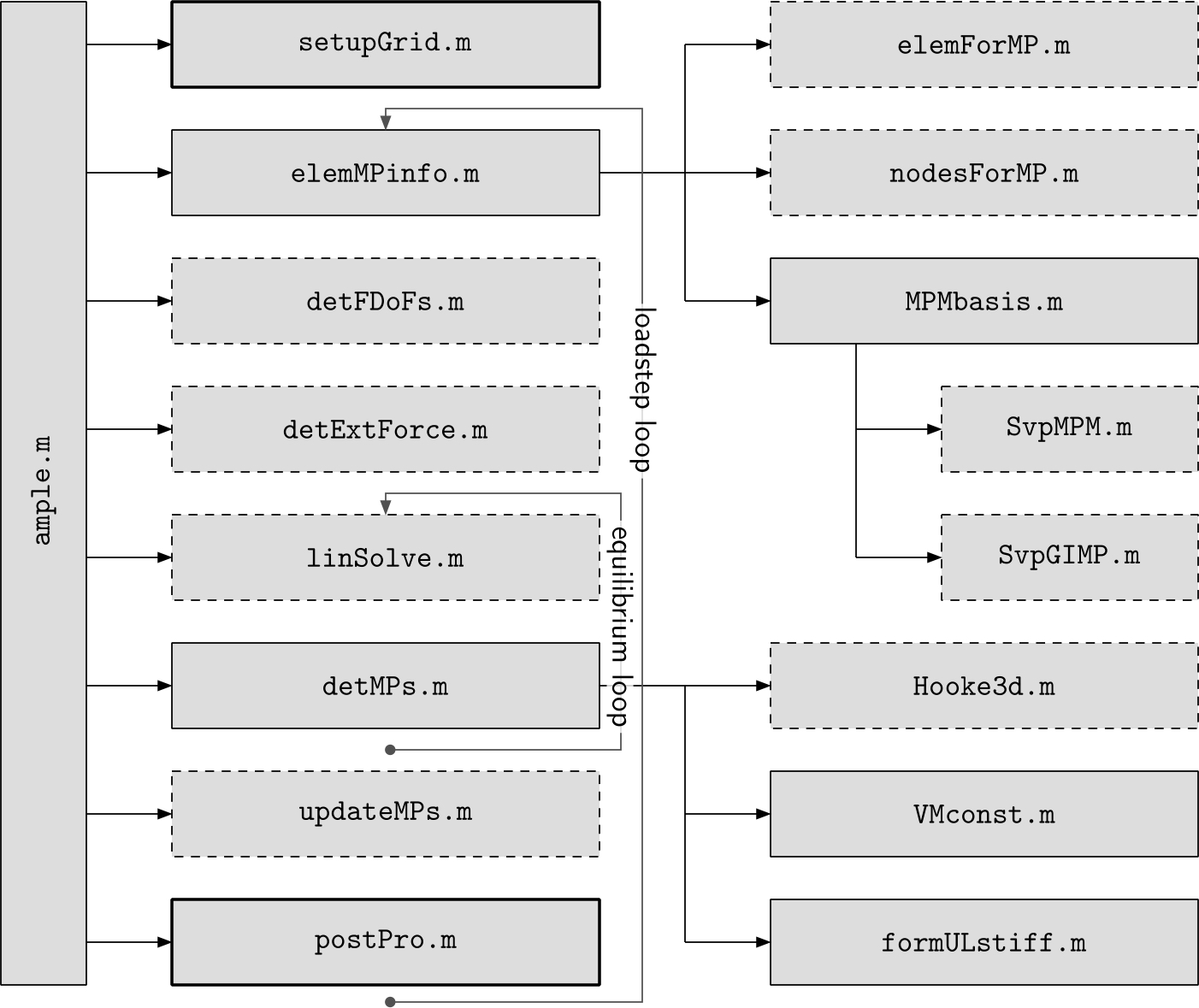
All of AMPLE’s functions share a common file format. An example AMPLE function is shown below, specifically the function to determine the external forces on the background mesh based on body and point forces at material points, detExtForce.m, which is called on line 12 of ample.m. The function starts with a common comment block that includes the following information: (i) brief description/title; (ii) author and date information with a more detailed description of the function’s purpose; (iii) function call format; (iv) required input information; (v) the function’s output; and (vi) a see also section detailing the functions that are called by the function (in the case of detExtForce.m, none).
Data Structures
The majority of the analysis information required by AMPLE is stored in two structured arrays:
-
mpData: that contains material point information, such as the point’s position, deformation gradient, Cauchy stress, etc.
-
mesh: that contains information about the background mesh, such as the positions of the nodes and the topology of each of the background mesh elements.
MATLAB’s structured arrays provide a convenient way to store the material point data as different material points will potentially influence different numbers of nodes and therefore will require different amounts of storage for, for example, the basis functions that influence the point and their spatial derivatives.