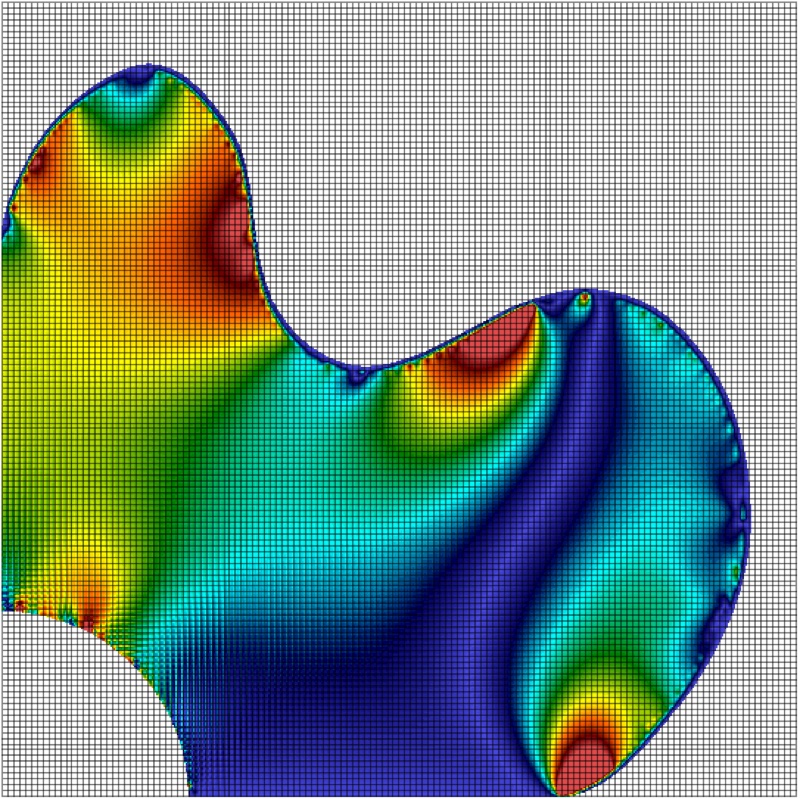
Numerical approaches based on Lagrangian mechanics, particularly using the finite element method, dominate the analysis of solid mechanics problems. However there are issues with mesh-based Lagrangian approaches for problems involving very large deformation in that the discretisation used to analyse the physical problem becomes distorted leading to inaccurate results and, in extreme cases, eventual breakdown of the numerics due to element inversion.

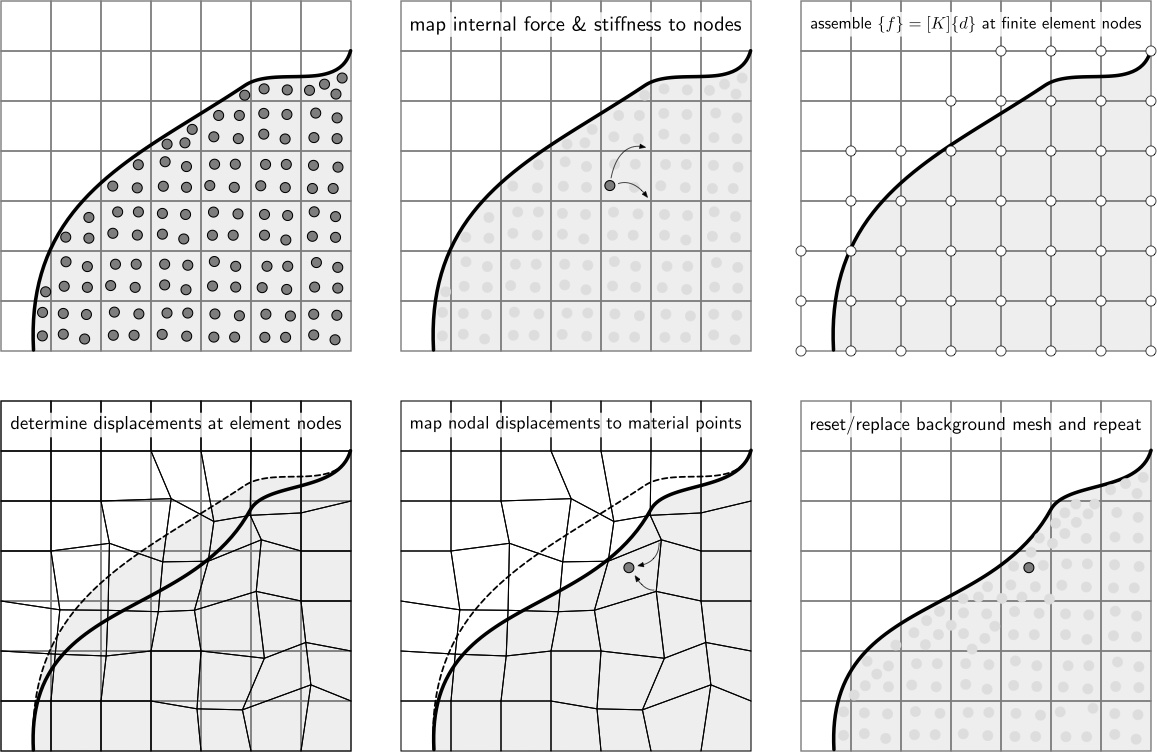
The Material Point Method (MPM) is an alternative to pure Lagrangian approaches and is well suited to problems involving very large deformations. The method was developed in the 1990’s by Sulsky et al. [1] as a solid mechanics extension to the FLuid Implicit Particle (FLIP) method [2] which itself was developed from the Particle-In-Cell (PIC) method [3]. In the material point method, equilibrium computations take place on a background grid but the calculations are based on information (mass, volume, stress, state variables, etc.) held at material points that are convected through the background grid as the material deforms. This allows computations to take place on an undistorted background mesh (structured or unstructured) whilst modelling problems involving very large deformations. One way to summarise the material point method is: a finite element method where the integration points (material points) are allowed to move independently of the mesh.

AMPLE, unlike most of the MPM community, adopts an implicit formulation. The key steps in an implicit implementation of the material point method are shown below.

---

[1] D. Sulsky, Z. Chen, H. Schreyer, A particle method for history-dependent materials, Computer Methods in Applied Mechanics and Engineering 118 (1994) 179–196.
[2] J.U. Brackbill, H.M. Ruppel, FLIP - A method for adaptively zoned, particle-in-cell calculations of fluid flows in two dimensions, Journal of Computational Physics 65 (1986), 314-343.
[3] F. Harlow, The particle-in-cell computing method for fluid dynamics, Methods for Computational Physics 3 (1964).

AMPLE: A Material Point Learning Environment

AMPLE was developed to address the sevre learning curve for researchers wishing to understand, and start using, the material point method. The software was developed at Durham University between 2014 and 2018 by Dr Will Coombs as a platform to test our new research ideas and understand the impact of adopting different material point variants. AMPLE was first released in January 2019 at the 2nd International Conference on the Material Point Method held at Cambridge University, UK.