AMPLE was developed with the following principles:

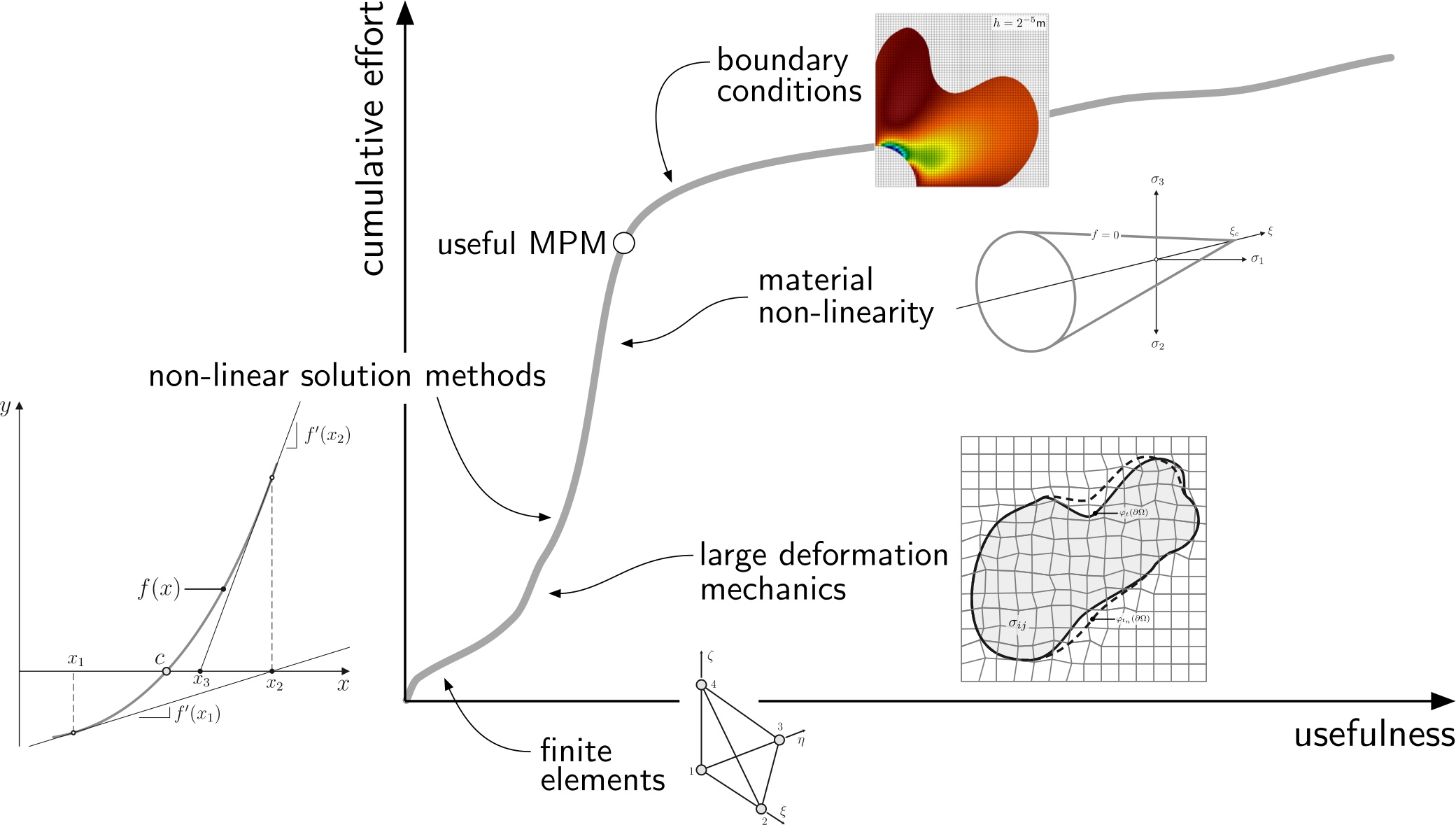
• MATLAB-based - the material point method is complex in that in order to implement a useful MPM code it is necessary for the developer to understand: finite element analysis, large deformation mechanics, non-linear solution methods and material non-linearity (elasto-plasticity). This results in a very steep learning curve (see below) and if users/developers have to understand thousands of lines of Fortran/C/C++ code the hurdle may become insurmountable for some. AMPLE has been developed in MATLAB to remove, or at least significantly lessen, the syntax learning curve.

• Compact - inspired by Nick Trefethen’s philosophy of ten digit algorithms: “…a little gem of a program to compute something numerical: Ten digits, Five seconds, And just one page” [1]. If a program is compact enough to be viewed on a single page it allows the structure of the whole algorithm to be understood and visualised, making mistakes and misunderstandings far less likely.

• Modular & expandable - AMPLE has been written as a series of compact functions called by a core analysis script. For example, the link between the material points and the background mesh is contained within one function and all of the other functions remain unchanged if the background mesh is changed. The continuum mechanics formulation is contained in another function and the material model (stress-strain relationship) in another. This allows users/developers to quickly understand the purpose of each of the functions and adapt/modify/replace functions as required.

• Rigorous - all aspects of AMPLE have been verified and are based on a rigorous updated Lagrangian continuum mechanics framework. The implemented algorithms are based on published material, including convergence analysis to ensure that the fundamentals of the code our sound. This should provide confidence when using/expanding AMPLE.

• Proof rather than performance - it is well documented that MATLAB is not as computationally efficient as compiled languages (such as Fortran or C/C++). However, the focus of AMPLE is on proof of new concepts and ideas, not high performance computations. It provides a environment for researchers to understand the material point method and test out new ideas.

---

[1] L.N. Trefethen (2005), Ten Digit Algorithms, Numerical Analysis Report 05/13, Oxford University.

AMPLE: A Material Point Learning Environment

AMPLE was developed to address the sevre learning curve for researchers wishing to understand, and start using, the material point method. The software was developed at Durham University between 2014 and 2018 by Dr Will Coombs as a platform to test our new research ideas and understand the impact of adopting different material point variants. AMPLE was first released in January 2019 at the 2nd International Conference on the Material Point Method held at Cambridge University, UK.